Leetcode算法之二叉树

105. 从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

思路：
（1）前序遍历：根节点->左节点->右节点；中序遍历：左子树->根节点->右子树
（2）利用前序遍历中的根节点将中序遍历数组拆分成俩部分，分别为当前根节点的左子树和右子树
（3）递归解决每个根节点的左子树和右子树问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
// 递归写法
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        if(preorder.size() == 0)
            return NULL;
        TreeNode* root = new TreeNode(preorder[0]);
        int pos = 0;
        while(pos < inorder.size() && preorder[0] != inorder[pos])
            pos++;

        vector<int> prev(preorder.begin()+1, preorder.begin()+pos+1);
        vector<int> inv(inorder.begin(), inorder.begin()+pos);
        root->left = buildTree(prev, inv);

        prev.assign(preorder.begin()+pos+1, preorder.end());
        inv.assign(inorder.begin()+pos+1, inorder.end());
        root->right = buildTree(prev, inv);

        return root;
    }
};

//迭代
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        if(preorder.size() == 0)
            return NULL;
        TreeNode* root = new TreeNode(preorder[0]);
        int pos = 0;
        stack<TreeNode*> st;
        st.push(root);
        for(int i = 1; i < preorder.size(); ++i)
        {
            int pval = preorder[i];
            TreeNode* node = st.top();
            if(node->val != inorder[pos])
            {
                node->left = new TreeNode(pval);
                st.push(node->left);
            }
            else
            {
                while(!st.empty() && st.top()->val == inorder[pos])
                {
                    node = st.top();
                    st.pop();
                    pos++;
                }
                node->right = new TreeNode(pval);
                st.push(node->right);
            }
        }
        return root;
    }
};

662. 二叉树最大宽度

给定一个二叉树，编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树（full binary tree）结构相同，但一些节点为空。

每一层的宽度被定义为两个端点（该层最左和最右的非空节点，两端点间的null节点也计入长度）之间的长度。

1
2
3
4
5
6
7
8
9
10
输入: 

           1
         /   \
        3     2
       / \     \  
      5   3     9 

输出: 4
解释: 最大值出现在树的第 3 层，宽度为 4 (5,3,null,9)。

思路：

  1. 求最大宽度，那么如果我们能求到最靠近左边的节点，保存下标；然后求得最后边的节点，利用下标之差，注意这个节点的父亲节点的父亲节点可能存在左子树。
  2. 题目有提到说类似于满二叉树结构，所以如果根节点下标设为i(i>=1)，那么根节点的左节点2 *i,右节点2 *i+1;
  3. 使用一个map来存放每一层最左边的节点的下标
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    class Solution {
    public:
        unsigned long long maxwidth = 0;
        map<int, unsigned long long> mp;
        void dfs(TreeNode* root, int level, unsigned long long index)
        {
            if(root == NULL)
                return;
            if(!mp.count(level))
                mp[level] = index;
            maxwidth = max(maxwidth, index - mp[level] + 1);
            dfs(root->left, level+1, index*2+1);
            dfs(root->right, level+1, index*2+2);
        }
        int widthOfBinaryTree(TreeNode* root) {
            dfs(root, 0, 0);
            return maxwidth;
        }
    };// 非递归
    class Solution {
    public:
        int maxwidth = 0;
        
        int widthOfBinaryTree(TreeNode* root) {
            if(root == NULL)
                return maxwidth;
            queue<pair<TreeNode*, int>> qt;
            vector<int> start;
            qt.push(pair<TreeNode*, int>(root, 1));
            while(!qt.empty())
            {
                pair<TreeNode*, int> p = qt.front();
                start.push_back(p.second);
                for(int i = 0; i < qt.size(); ++i)
                {
                    pair<TreeNode*, int> tp = qt.front();
                    qt.pop();
                    maxwidth = max(maxwidth, tp.second - p.second + 1);
                    if(tp.first->left)
                        qt.push(pair<TreeNode*, int>(tp.first->left, 2*tp.second));
                    if(tp.first->right)
                        qt.push(pair<TreeNode*, int>(tp.first->left, 2*tp.second+1));
                }
            }
            return maxwidth;
        }
    };

543. 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

1
2
3
4
5
    1
   / \
  2   3
 / \     
4   5

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意：两结点之间的路径长度是以它们之间边的数目表示。
思路：

  1. 直径的概念：俩个节点之间的路径长度，对于每一个节点来说，就是左子树长度+右子树长度
  2. 求最大直径，比较所有节点的直径，取最大值
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    class Solution {
        int ans;
        int diameter(TreeNode* root) 
        {
            if(root == NULL) return 0;
            int l = diameter(root->left);
            int r = diameter(root->right);
            ans = max(ans, l + r);
            return max(l,r) + 1;
        }
    public:
        int diameterOfBinaryTree(TreeNode* root) {
            ans = 0;
            diameter(root);
            return ans;
        }
    };

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

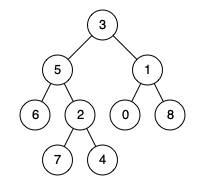
例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

](https://img-blog.csdnimg.cn/20200908085259995.png#pic_center)

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

思路：
分析二叉树的结构，左子树，右子树， 根节点，给定俩个节点，找最近公共祖先
（1）当某一节点A在另一节B点的左子树或右子树中，则B为最近公共祖先，反之亦然
（2）如果一个节点C的左子树和右子树分别包含A，B节点，则C为AB的公共祖先，那么如何保证C为最近公共祖先呢？当我们采用递归的方式查找（递归到叶子节点回退判断）的时候，最先查找的节点就是最近的点，直接返回即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    TreeNode* ans;

    bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        if(root == NULL) return false;
        bool lson = dfs(root->left,p,q);
        bool rson = dfs(root->right,p,q);
        if((lson && rson) || ((root->val == p->val) || root->val == q->val) && (lson || rson))
            ans = root;
        return lson || rson || (root->val == p->val || root->val == q->val);
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
    {
        dfs(root, p, q);
        return ans;
    }
};

257. 二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。

1
2
3
4
5
6
7
8
输入:
   1
 /   \
2     3
 \
  5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3

思路：

  1. 回溯的方法
  2. 使用vector先存储，存完后转string
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    class Solution {
    public:
        vector<string> path;

        vector<string> binaryTreePaths(TreeNode* root) {
            vector<int> vc;
            TreePath(root,vc);
            return path;
        }
        void TreePath(TreeNode* root, vector<int>& vc)
        {
            if(root == NULL)
                return;
            vc.push_back(root->val);
            if(root->left == NULL && root->right == NULL)
            {
                string str = "";
                for(int i = 0; i < vc.size(); ++i)
                {
                    cout << vc[i];
                    str += to_string(vc[i]);
                    if(i != vc.size()-1)
                        str += "->";
                }
                cout << endl;
                path.push_back(str);
                vc.pop_back();
                return;
            }
            TreePath(root->left, vc);
            TreePath(root->right, vc);
            vc.pop_back();
        }
    };
数据结构与算法
#Leetcode
Leetcode算法之二叉树
http://example.com/2023/10/25/Leetcode算法之二叉树/
作者
Whlok
发布于
2023年10月25日
许可协议